Mechanistic Model
Consider a feedforward input-output system, consisting of three identical input cells, with theirs center at \( \mathbf{r}_{\beta_1}, \mathbf{r}_{\beta_2}\) and \(\mathbf{r}_{\beta_3}\), and one output cell at \(\mathbf{r}_{\alpha}\).
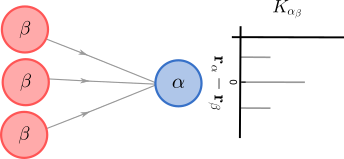
Finite number of input cells.
It is clear that the activity of the output cell will depend on the activity of the input cells. By using the linear descriptive model as inspiration we can relate the response of the output cell to that of the input cells:
\begin{align} R_\alpha(\mathbf{r}_\alpha,t) = R_{0,\alpha} + \sum_j \int_\tau K_{\alpha \beta}(\mathbf{r}_{\alpha} - \mathbf{r}_{\beta_j}, \tau) R_\beta(\mathbf{r}_{\beta_j},t - \tau) \mathrm{d}\tau, \end{align}
where the sum goes over all input cells and \(R_{0,\alpha}\) accounts for any background firing that may occur when there is no input (assumed to be stationary). The couplings function \(K_{\alpha\beta}(\mathbf{r}_{\alpha} - \mathbf{r}_{\beta}, \tau)\) denotes the sign and strength with which the response of the input cell \(\beta\), at a distance \(\mathbf{r}_{\alpha} - \mathbf{r}_\beta\) from the output cell \(\alpha\), at time \(t-\tau\) influences the response of the output cell at time \(t\). Note that \(K_{\alpha\beta}(\mathbf{r}_{\alpha} - \mathbf{r}_{\beta}, \tau) = 0\) for all values \(\tau < 0\), so that the integral may be taken from \(-\infty\) to \(+\infty\).
If one hypothetically considers a large number of densely and evenly distributed cell inputs (from identical cells) to the output cell, the spatial discrete coupling function can as an approximation be replaced with a spatial continuous coupling function (see figure below).
\begin{equation} R_\alpha(\mathbf{r}_\alpha,t) = R_{0,\alpha}+ \displaystyle\int_{\tau} \iint_\mathbf{r} K_{\alpha\beta}(\mathbf{r}_{\alpha} - \mathbf{r},\tau) R_\beta(\mathbf{r},t - \tau) \mathrm{d}^2\mathbf{r}\mathrm{d}\tau, \end{equation}
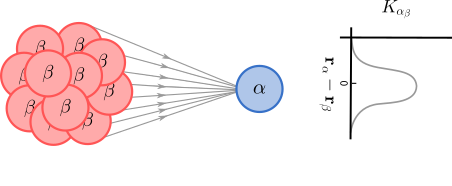
A large number of densely and evenly distributed input cells.