Fourier Transform
The repsponse and impulse response integrals can be evaluated by using Fourier transform. This is much more efficent since complexity of computing is reduced from \( O(n^2) \), which arises if one simply applies the definition of discrete Fourier transform, to \( O(n \log n) \), where \(n \) is the data size.
Continuous Fourier Transform
The (continuous) Fourier transform (CFT) of a signal and its inverse Fourier transform are given by
\begin{equation} \tilde{y}(k,\omega) = \displaystyle\int_{t} \int_x e^{-i(kx - \omega t)}y(x, t) \mathrm{d}x\;\mathrm{d}t, \end{equation}
\begin{equation} y(x,t) = \frac{1}{(2\pi)^3} \displaystyle\int_{\omega} \int_k e^{i(kx - \omega t)}\tilde{y}(k, \omega) \mathrm{d}k\;\mathrm{d}\omega. \end{equation}
Discrete Fourier Transform
The discrete Fourier transform (DFT) is defined as
\begin{align} \widetilde{Y}_{m'n'} = \sum_{m,n} Y_{m,n} \exp \bigg( -2\pi i \bigg( \frac{m'm}{M} -\frac{n'n}{N} \bigg) \bigg) \end{align}
\begin{align} Y_{m,n} &= \sum_{m'n'} \widetilde{Y}_{m'n'} \exp \bigg( 2\pi i \bigg( \frac{m'm}{M} -\frac{n'n}{N} \bigg) \bigg) \end{align}
There are several techniques for computing the DFT, and these are referred to as fast Fourier transform (FFT) algorithms.
Relationship between spatiotemporal-domain and frequency-domain
| Spatial | Time | |
|---|---|---|
| Number of samples | \(M \) | \(N \) |
| Resolution | \(\Delta x \) | \(\Delta t \) |
| Max | \(L = M \Delta x \) | \(T = N \Delta t \) |
| Sampling frequency | \(k_s = \frac{2\pi}{\Delta x} \) | \(\omega_s = \frac{2\pi}{\Delta t} \) |
The accuracy of DFT is determined by two fundamental numbers
| Spatial | Time | |
|---|---|---|
| Max frequency (Nyquist) | \(k_{\mathrm{max}} = \frac{k_s}{2} = \frac{2\pi}{2\Delta x} = 2\pi\frac{M}{2 L} \) | \(\omega_{\mathrm{max}} = \frac{f_s}{2} = \frac{2\pi}{2\Delta t} = 2\pi\frac{N}{2 T} \) |
| Frequency resolution | \(\Delta k = \frac{2\pi}{L} = \frac{k_s}{M}\) | \(\Delta \omega = \frac{2\pi}{T} = \frac{f_s}{N}\) |
From the relations above we also get the important relation between the resolution in time-domain and frequency domain.
\begin{align} \boxed{ \Delta x \Delta k = \frac{2\pi}{M} \quad \quad \quad \Delta t \Delta \omega = \frac{2\pi}{N} } \end{align}
Discretized Continuous Fourier transform
Consider an arbitary continuous function \(y(x,t) \) sampled in an even numbers \(M\) and \(N\) of points in spatial and time, respectively, with a sampling resolution of \(\Delta t\) and \(\Delta x\) . The discretized grid is given by
\begin{align} x &= m \Delta x - \frac{L}{2}, \quad m = \left\{0, \dots, M-1 \right\} \\ t &= n \Delta t, \quad n = \left\{0, \dots, N-1 \right\} \end{align}
The corrosponding DFT sample frequencies are
\begin{align} k &= m' \Delta k, \quad m' = \left\{0, \dots, M-1 \right\}\\ \omega &= n' \Delta \omega, \quad n' = \left\{0, \dots, N-1 \right\} \end{align}
Forward Fourier transform
\begin{align} \tilde{y}(k,\omega) &= \displaystyle\int_x \int_{t} e^{-i(kx - \omega t)} y(x,t) \mathrm{d}t\;\mathrm{d}x \\ \tilde{y}(m' \Delta k, n' \Delta \omega) &\approx \sum_{m,n} \Delta x \Delta t \; y(m \Delta x - \frac{L}{2}, n \Delta t) \exp \bigg( -i \bigg( m' \Delta k \; (m \Delta x - \frac{L}{2}) - n' \Delta \omega \; n \Delta t \bigg)\bigg) \\ &= \Delta x \Delta t\exp \bigg(i m' \Delta k \frac{L}{2} \bigg) \sum_{m,n} y(m \Delta x, n \Delta t) \exp \bigg( -2\pi i \bigg( \frac{m'm}{M} -\frac{n'n}{N} \bigg) \bigg) \\ &= \Delta x \Delta t (-1)^{m'} \widetilde{Y}_{m'n'} \end{align}
Backward Fourier transform
\begin{align} y(x,t) &= \frac{1}{(2\pi)^2} \displaystyle\int_k \int_{\omega} e^{i(kx - \omega t)} \tilde{y}(k,\omega) \mathrm{d}\omega\;\mathrm{d}k \\ y(m \Delta x - \frac{L}{2}, n \Delta t) &\approx \frac{1}{(2\pi)^2}\sum_{m'n'} \Delta k \Delta \omega \; \tilde{y}((m' \Delta k, n' \Delta \omega) \exp \bigg( i \bigg( m' \Delta k \; (m \Delta x - \frac{L}{2}) - n' \Delta \omega \; n \Delta t \bigg)\bigg) \\ &= \frac{\Delta k \Delta \omega }{(2\pi)^2}\sum_{m'n'} \tilde{y}(m' \Delta k, n' \Delta \omega) \exp \bigg( 2\pi i \bigg( \frac{m'm}{M} -\frac{n'n}{N} \bigg) \bigg) \exp \bigg(-i m' \Delta k \frac{L}{2} \bigg) \\ &= \frac{\Delta k \Delta \omega }{(2\pi)^2}\sum_{m'n'} \tilde{y}(m' \Delta k, n' \Delta \omega) \exp \bigg( 2\pi i \bigg( \frac{m'm}{M} -\frac{n'n}{N} \bigg) \bigg) (-1)^{m'} \end{align}
Note: Often in the FFT implementations the resulting values follow the so-called "standard" order. In the one dimensional case the first element in the resulting array is the zero-frequency term (DC term). Then element (using Python indexing) \( \{1, N/2 -1\} \) contains the positive-frequency terms, and \(\{N/2, N-1\}\) contains the negative-frequency terms, in order of decreasingly negative frequency.
Two-Dimensional Frequency Spectrum
Taking the Fourier transform of an \(M_x \times M_y\) image decompose the image into its sine and cosine components. In the figure below the corresponding frequency spectrum is shown.
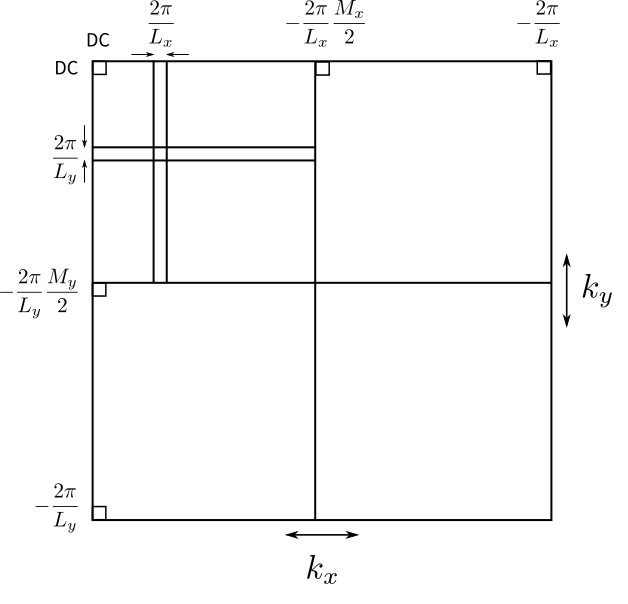
The frequency spectrum.