The dLGN Circuit
In this section we derive the impulse-response function for the thalamic relay cells using the mechanistic model and based on current knowledge about the neuronal connectivity in dLGN. The focus of attention is the firing rate of dLGN relay cells with ON symmetry. These neurons receive feedforward excitation and indirect feedforward inhibition (via intrageniculate interneurons) from ON-center ganglion cells in retina. The relay cells further receive cortical feedback from both cortical ON cells and cortical OFF cells. The cortical feedback can be both excitatory (direct) and inhibitory (indirect via intrageniculate interneurons). The cortical ON and OFF cells are in turn assumed to be driven by the ON and OFF relay cells, respectively.
The corticogeniculate feedback comes from orientation-tuned cells in layer 6 in cortex. We consider a set of \(N\) mutually uncoupled, orientation-selective cortical populations \(\text{C}_n\), for \(n=1, 2,\dots, N\), for both ON and OFF pathways. Each population \(\text{C}_n\) responds preferably to stimuli (bars, gratings) with orientation \(\theta_n\). In figure below only one cortical population is shown for each pathway even though an arbitrary number of cortical populations is considered.
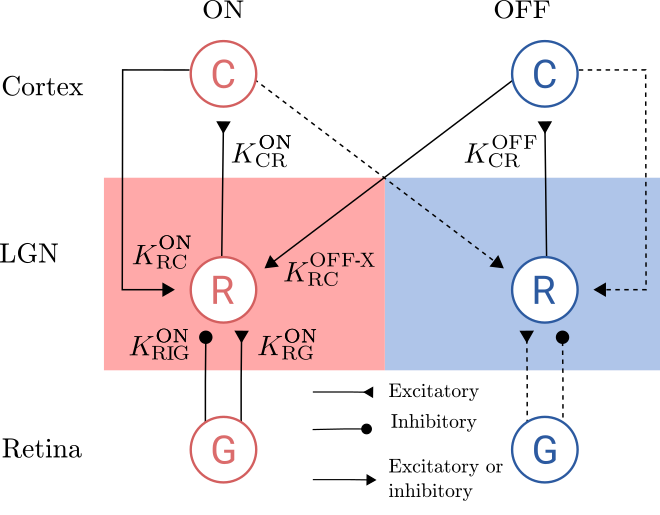
dLGN circuit.
The firing-rate responses (ON-pathway) of the various cells in the early visual pathway are assumed to be governed by the following set of equations:
\begin{align} R_\mathrm{G}^{\mathrm{ON}}(\mathbf{r},t) &= W^{\mathrm{ON}}_{\mathrm{G}}(\mathbf{r},t) \otimes S(\mathbf{r},t), \\ R^{\mathrm{ON}}_\mathrm{C}(\mathbf{r},t) &= K^{\mathrm{ON}}_{\mathrm{C} \mathrm{R}}(\mathbf{r},t) \otimes R^{\mathrm{ON}}_{\mathrm{R}}(\mathbf{r},t), \\ R^{\mathrm{ON}}_\mathrm{R}(\mathbf{r},t) &= K^{\mathrm{ON}}_{\mathrm{R}\mathrm{G}}(\mathbf{r},t) \otimes R^{\mathrm{ON}}_{\mathrm{G}}(\mathbf{r},t) \\ &+K^{\mathrm{ON}}_{\mathrm{R}\mathrm{I} \mathrm{G}}(\mathbf{r},t) \otimes R^{\mathrm{ON}}_{\mathrm{G}}(\mathbf{r},t) \\ &+\sum_{n}K^{\mathrm{ON}}_{\mathrm{R} \mathrm{C}_n}(\mathbf{r},t) \otimes R^{\mathrm{ON}}_{\mathrm{C}_n}(\mathbf{r},t) \\ &+\sum_{n}K^{\mathrm{OFF-X}}_{\mathrm{R} \mathrm{C}_n}(\mathbf{r},t) \otimes R^{\mathrm{OFF}}_{\mathrm{C}_n}(\mathbf{r},t). \end{align}
Phase-reversed push-pull cortical feedback
The dLGN circuit exhibits various nonlinear effects. In order to include some of these effects the response of the cortical cells are expressed as a nonlinear function of the linearly filtered input. More specifically we express the response of the (ON or OFF) cortical population \( \text{C}_n\) by
\begin{equation} R^{\text{ON/OFF}}_{\mathrm{C}_n} \;\;\; = \left[K^{\text{ON/OFF}}_{\mathrm{C}_n \mathrm{R}} \otimes R^{\text{ON/OFF}}_{\mathrm{R}}\right]_{+}, \end{equation}
where \([x]_+\) is the half-wave rectification function (\([x<0]_+ = 0, [x\ge0]_+=x\), and \(K^{\text{ON/OFF}}_{\mathrm{C}_n \mathrm{R}}\) is the feedforward kernel between the relay cells and the cortical cells in population \(\text{C}_n\). We further assume the input to cortical OFF cells to be the negative of the one for the ON cells. That is
\begin{equation} R^{\text{OFF}}_{\mathrm{C}_n} = \left[-K^{\text{ON}}_{\mathrm{C}_n \mathrm{R}} \otimes R^{\text{ON}}_{\mathrm{R}}\right]_{+}. \end{equation}
Finally, the feedback kernels are assumed to be related by (phase-reversal)
\begin{equation} K^{\text{OFF-X}}_{\mathrm{R}\mathrm{C}_n}\; = -K^{\text{ON}}_{\mathrm{R}\mathrm{C}_n}, \end{equation}
where \(K^{\text{OFF-X}}_{\mathrm{R}\mathrm{C}_n}\) is the cross-coupling feedback from cortical OFF cells onto relay ON cells. These assumptions are discussed carefully in Einevoll et al. 2012 [1].
Using the three assumptions above, the total input to the ON dLGN relay cell is given by
\begin{align} R^{\text{ON}}_\mathrm{R} &= K^{\text{ON}}_{\mathrm{R}\mathrm{G}} \otimes R^{\text{ON}}_{\mathrm{G}} +K^{\text{ON}}_{\mathrm{R} \mathrm{I}\mathrm{G}} \otimes R^{\text{ON}}_{\mathrm{G}} +\sum_nK^{\text{ON}}_{\mathrm{R} \mathrm{C}_n} \otimes R^{\text{ON}}_{\mathrm{C}_n} +\sum_nK^{\text{OFF-X}}_{\mathrm{R} \mathrm{C}_n} \otimes R^{\text{OFF}}_{\mathrm{C}_n} \\ &= K^{\text{ON}}_{\mathrm{R}\mathrm{G}} \otimes R^{\text{ON}}_{\mathrm{G}} +K^{\text{ON}}_{\mathrm{R} \mathrm{I}\mathrm{G}} \otimes R^{\text{ON}}_{\mathrm{G}} +\sum_nK^{\text{ON}}_{\mathrm{R} \mathrm{C}_n} \otimes K^{\text{ON}}_{\mathrm{C}_n \mathrm{R}} \otimes R^{\text{ON}}_{\mathrm{R}}, \end{align}
where we have used the mathematical identity: \([x]_+ -[-x]_+ = x\). By inserting the expression for the descriptive model for \(R^{\text{ON}}_\mathrm{R}\) and \( R^{\text{ON}}_\mathrm{G}\), and applying the convolution theorem we obtain
\begin{align} \widetilde{W}^{\text{ON}}_\mathrm{R} \widetilde{S} &= \left( \widetilde{K}^{\text{ON}}_{\mathrm{R}\mathrm{G}}\widetilde{W}^{\text{ON}}_{\mathrm{G}} +\widetilde{K}^{\text{ON}}_{\mathrm{R} \mathrm{I}\mathrm{G}}\widetilde{W}^{\text{ON}}_{\mathrm{G}} +\sum_n \widetilde{K}^{\text{ON}}_{\mathrm{R} \mathrm{C}_n} \widetilde{K}^{\text{ON}}_{\mathrm{C}_n \mathrm{R}} \widetilde{W}^{\text{ON}}_{\mathrm{R}} \right) \widetilde{S}, \end{align}
Comparing both sides of the equal sign we see that
\begin{align} \widetilde{W}^{\text{ON}}_{\mathrm{R}} &=\frac{ \widetilde{K}^{\text{ON}}_{{\mathrm{R}} \mathrm{G}} +\widetilde{K}^{\text{ON}}_{\mathrm{R} \mathrm{I}\mathrm{G}} } { 1 -\sum_n\widetilde{K}^{\text{ON}}_{\mathrm{R} \mathrm{C}_n}\widetilde{K}^{\text{ON}}_{\mathrm{C}_n \mathrm{R}} }\; \widetilde{W}^{\text{ON}}_{\mathrm{G}}. \end{align}
In this expression the direct feedforward excitation and the indirect feedforward inhibition via interneurons are represented by the first and second terms in the numerator, respectively. The feedback effects are accounted for in the denominator.
References
[1] Einevoll, Gaute T., and Hans E. Plesser. "Extended difference-of-Gaussians model incorporating cortical feedback for relay cells in the lateral geniculate nucleus of cat." Cognitive neurodynamics 6.4 (2012): 307-324.
[2] Wang, Wei, et al. "Functional alignment of feedback effects from visual cortex to thalamus." Nature neuroscience 9.10 (2006): 1330-1336.
[3] Norheim, Eivind S., et al. "A minimal mechanistic model for temporal signal processing in the lateral geniculate nucleus." Cognitive Neurodynamics 6.3 (2012): 259-281.